명리학 학원 사주위키 (갤러리)
천간, 지지, 간지의 주기 본문
최근에 사주 명리학 과외 수강생 한 분이 졸업하셨습니다.
사주 상담을 받으러 오셨다가 명리학 과외까지 받게 되신 분이신데요?
첫 상담 때 H 선생님의 60년 주기 이론이 타당한지 아닌지를 물어보시더라고요?
그래서 제가 명리학에는 10년 주기, 12년 주기는 있어도
60년이 통으로 된 주기는 없다는 말씀을 드렸었습니다.
그런 주기는 H 선생님이 독창적으로 만드신 것이라는 이야기를 드렸죠.
최종적으로 10주기와 12주기 그래프를 합성한
60년 주기는 있을 수 있다는 말씀을 드렸었습니다.
스승의 날 선물도 주시고 가셨으니
저도 졸업 선물로 그림 4장 그려 왔습니다.

기본적인 sin, cos 함수는 -1부터 +1까지 진동합니다.
x축을 개(開)직선으로 두었습니다.

x축을 폐(閉)곡선으로 말아주면 이렇게 됩니다.
360도를 쓰면 헷갈리실 까봐 60분법으로 수정해왔습니다.

그런데 명리학에서는 음양이 0부터 2까지 진동합니다.
적어도 그렇게 해야 이해하기가 쉽습니다.
예를 들어서 오행의 강약을 시각화할 때
극신강한 사주를 +100%라고 하면
양의 부피라서 상상할 수 있습니다.
그러나
극신약한 사주를 -100%라고 하면
음의 부피라서 상상하기가 어렵습니다.
제가 설명하기도 어렵고요.
그래서 그냥
극신약한 사주 = 0%에 가깝다.
극신강한 사주 = 200%에 가깝다.
라고 하면 둘 다 양의 부피라
상상하기도, 그려서 설명하기도 훨씬 쉬워지죠.
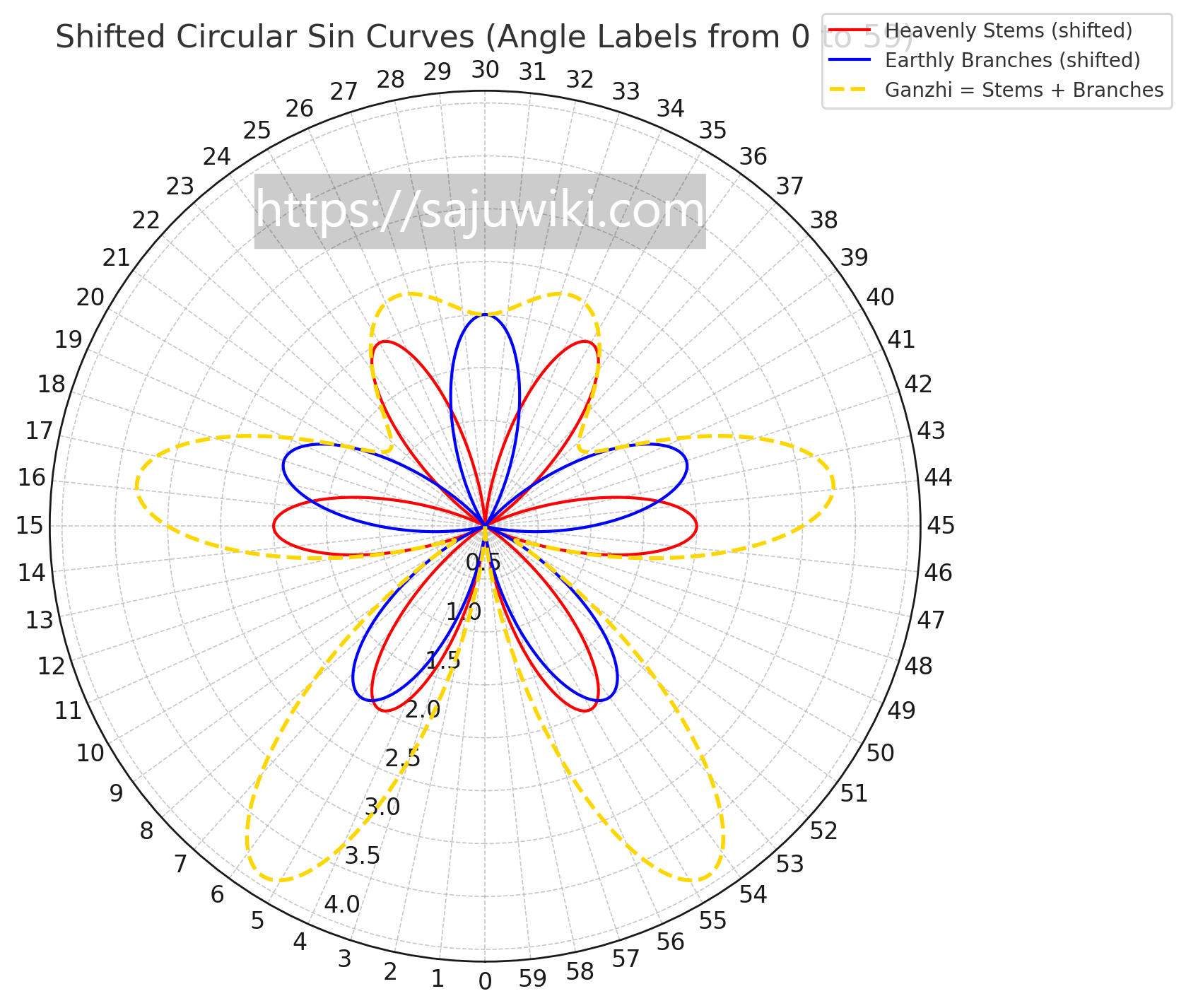
이번에도 둥글게 말아주면 이런 식으로 되는데요?
이런 표현 방식을 극좌표계(polar coordinate system)라고 합니다.
r과 θ(세타)로 표현되죠.
차이점이 또 하나 있다면
일반적인 극좌표계는 우측이 0도이고 반시계방향으로 도는데
역학에 적합한 극좌표계는 아래가 0도이고 시계방향으로 돈다는 점입니다.
초반 두 그림과 후반 두 그림이
비슷해 보이면서도 조금 다르죠?
그래도 충분히 유용하게 이해하실 수 있으리라고 믿습니다.
위 그림은 단순히 10천간과 12지지에 대한 그림이 아닙니다.
12주기는 다들 아시다시피 십이운성 이론과도 일치합니다.
10주기는 제가 네이버 블로그에서 주장했던 십유성 이론과 일치합니다.
천간은 인접한 지지에 따라 12주기를 띠고
지지는 인접한 천간에 따라 10주기를 띱니다.
졸업 후에도 열공하시기 바랍니다.
7월 중에 종로 3가역 도보 5분 거리
육의전빌딩 7층에서 대형 강의실을 사용하게 되었으니 또 만납시다.
그때까지 임상도 많이 해 보시고요 ^^
'상담 및 수업' 카테고리의 다른 글
| 사주위키 운세 그래프 사용 설명서 (4) | 2025.06.07 |
|---|---|
| 영생 이전의 철학과 영생 이후의 철학적 그래프 (4) | 2025.06.04 |
| 운세 그래프는 연속적인가? 불연속적인가? (4) | 2025.06.01 |
| 대운 년운 월운 소운 일운 시운의 주기 (0) | 2025.05.21 |
| 별 모양 오각형 프랙탈에 오행을 입히면 사상이 보인다. (2) | 2025.03.02 |




